本年 4月の本格的な共同利用開始からまだ 6 ヶ月しか経っておらず，また，ワークステーション上でのシーケンシャルなスカラ計算に慣れてしまったユーザにとってベクトル化・並列化のプログラミングはかなり取っ付きにくいものであるため，VPP システムを使用した研究成果が出揃うにはしばしの時間が掛かりそうである。

しかしもちろん，各ユーザはそれなりの展望と指針を持って己の計算を進めており，そのいくつかからは既に注目すべき学術的な結果が出つつある。ここでは，そのような数少ない例の中から，VPP システムの最大の特徴である並列化を駆使した数値計算の結果についていくつか紹介し，将来への展望を探ってみることにする。

流体運動の並列数値解法

流体力学の基礎方程式はその強い非線型性から解析的な扱いが困難であり，計算機の能力が発達し出す今日までその需要の多さにも関わらず詳細な解析が進められなかった分野である。しかしまた，大行列を扱う流体力学の数値実験はスーパーコンピュータのようなベクトル計算機には非常におあつらえ向きな問題であり，ベクトル計算機の発展と共にあらゆる研究領域で流体力学の数値解法が開発され，次々と科学的成果が発表され続けて来た。

流体力学の数値解法はスーパーコンピュータの存在意義そのものであると言っても過言ではなかろう。そしていつの時代にも，天文学者は流体力学スーパーコンピューティングの最大手ユーザの一人であった。

計算機の上で流体を記述するには，座標上に固定された位置から流体の動きを眺めるEuler法と，流体と共に動く座標系で流体を記述するLagrange法とがある⁸⁾。 Euler法による流体力学の解法は非常にポピュラーであるし，本誌のかつての記事にも非常に興味深い詳細な解説が掲載されているので，関心のある方はそちらも参照されると良いだろう⁹⁾。

流体力学の伝統的数値解法はそれ自体で並列化に適したものが多いので，並列計算機が出て来たからと言って焦って新しい手法に飛び付かずとも，少しの工夫で今ある計算コードをうまく並列化することができる。

Euler法では空間に固定された格子を張り，それら格子上の各点での物理量の時間変化を追う。この時，或るステップnでの或る格子i上の物理量 xⁿ_iを求めるために必要となるのは，二次の陽解法を用いるとしてもせいぜい前の時刻におけるその格子とその前後の二点での情報 x^n-1_i-1，x^n-1_i，x^n-1_i+1の三個である。従って，計算領域が非常に広い場合には全体をいくつかの大きなまとまりに分割し，各まとまりをそれぞれ並列に計算することが可能になる。接触している境界部を除けば，各大領域の計算はどれも独立に扱うことができるからである。

具体的なアルゴリズムの例を模式化すると 図-4のようになる。これはある種の二次元流体モデルの時間発展計算の例を示したものであるが，数値流速の計算と各種保存量の時間積分において y方向を大領域に分割し，それぞれを独立のPEで並列に計算している。

図-4

このようにすることで計算速度は 1PEの非並列計算に比べて格段に向上するし(図-5)，大規模な主記憶を使用することで格子数を増やすことが可能になり，精度も大きく改善される。こうした手法を用いて計算した原始惑星系円盤の初期進化の一例を図-6に示した。

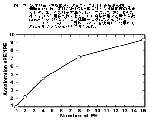図-5

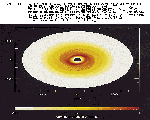図-6

ベクトル計算機の時代から流体力学の数値解法はスーパーコンピュータの需要の過半量を占めるものであったが，並列計算機の時代になってもその地位は揺るぎそうにない。天文学の分野でも多くの研究者が更なる計算速度と精度の改善に向けて新しい並列化・ベクトル化アルゴリズムを続々と開発しつつあり，今後ますますの発展が望まれている。

輻射輸送過程の並列計算

しかし，これだけ重要な意義を持ちながらも，輻射場と物質の相互作用を厳密に扱う輻射流体力学の理論はそもそも問題が高次元(空間三次元，方向二次元，波長一次元)であるために計算量が莫大になり，解析的な研究はもちろんのこと計算機の力不足が原因して数値計算すらろくに行われていないという状況が長く続いていた。

もちろん今までにも簡略化された仮定のもとでの数値計算が行われて来てはいたが，そうした計算は定量的に低精度であるばかりでなく，或る種の境界条件のもとでは定性的にまったく異なった解を与えてしまう場合もあることがわかっており，現在の天文学の要求レベルから考えて納得の行くものでは全然ない。

しかるに近年，並列計算に極めて適した輻射流体力学の計算アルゴリズムが開発されつつあり¹¹⁾,多次元空間における精密な輻射輸送計算も可能になりつつある(図-7)。図-7のスキームはプロセスAとプロセスBに分割されるが，ちょっとした見積もりをやってみればすぐにわかるように，これらのスキームのうち圧倒的に計算量が多いのはプロセスBであり，通常の非並列計算ではプロセスAの 100倍以上の計算時間を必要とする。

図-7

だがこのことは，我々にとってむしろ非常に都合が良い。プロセスAではShort Characteristic Methodと呼ばれる方法によって定常輻射輸送の方程式を解くのだが，この方法では空間を単位立方体の格子に分割し，各格子点上での輻射強度をすべての空間方向とすべての振動数に対して求めるという操作を行なう¹²⁾。この場合，各空間方向についての計算はそれぞれまったく独立に行うことができるし，各振動数についての計算も同様にすべて独立に行うことができる。すなわち，プロセスBで行われる計算は非常に効率良く並列化できることが期待されるのである。

いくつかの試験的な数値計算を行ってみたところ，計算速度の向上は予想通り非常に良いものであることがわかった(図-8)。試験計算の結果も示しておく(図-9)。この図は，立方体の中心に放射源を置き，そこから輻射輸送されるエネルギーを図-7のアルゴリズムを使ってVPP300で計算し，Power ONYX上のAVSを用いた三次元のボリュームレンダリングによって単位体積あたりの輻射エネルギー密度を描いたものである。

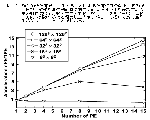図-8

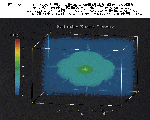図-9

理論的にはこの結果は純粋なる球対称分布を示すはずであるが，空間メッシュの数がまだ足りないために人工的な非球対称性が認められる。けれども，これでも従来の小規模計算の結果と比べれば計算の精度は格段に良くなっており，並列実行を行なうことによって計算速度も破格に向上している。

アルゴリズムやコーディングが更に洗練されるにつれて，より現実的な境界条件下での輻射輸送問題の計算が可能になり，星形成・惑星系形成における最大の難関であったこの問題に対する真正面からの取り組みが次第に現実味を帯びて行くものと期待される。

データ量の大小と並列化効果

図-10は富士通の科学技術計算ライブラリ集SSL IIのVPP版であるSSL II VPPに含まれる関数 dp_v2drcfのベンチマーク結果の一部¹³⁾である。明らかにPE台数効果が現われて来るのはせいぜいが 1,024×1,024程度の場合からで，それより小さなデータを扱った場合にはむしろ並列度を高めるごとに計算速度が低下してしまうことがわかる。いくらPEを多く使用しても，扱うデータ量が小さい場合には並列計算の効果がPE間通信というボトルネックによって打ち消されてしまうようである。

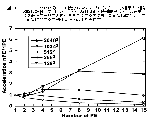図-10

扱うデータ量が大きくなければ大型計算機のメリットを生かすことができないという事実はベクトル計算機の時代からまったくの常識とされてはいたものの，並列計算においてもやはり同様にデータ量(配列サイズとも言い換えられる)の大きさは計算の効率を左右する大きなファクターのようである。まあ，我々はそのためにわざわざ巨大な主記憶を仕様として要求したのだから当然と言えば当然である。

けれども，だからと言ってVPPシステムが小規模なデータを扱う問題に対してまったく無力であるかというと，そんなことは決してない。現在，研究者にとって比較的簡単に手が届くPCやワークステーションにはPEが複数塔載されているものはほとんどないが，近い将来にはVPPシステムと同様に複数プロセッサを塔載したマシンが標準になり，並列計算を実行することで計算効率を高めて行くのが常識になるような時代が来るであろう。

その時代を先取りし，今から並列計算に適した専用の数値アルゴリズムを開発するためのプラットフォームとしてVPPシステムを利用するということも十分に考えられる。実際，表-1に掲載された国立天文台計算機利用研究プロジェクトの中には，それぞれの研究分野における並列計算用アルゴリズムを開発するプロジェクトもいくつか含まれている。この中で筆者自身が直接取り組んでいる重力少体問題の数値解法を並列化によって高速化する試みについて若干紹介したい。

並列化補外法による常微分方程式の高速解法

しかしながら，こうした重力少体問題(少数の質点の重力相互作用による問題という意味。よく使われる「重力多体問題」に対比して用いられる)はベクトル化や並列化が大変馴染みにくい分野とされて来た。何しろ扱う粒子(天体)の数が少ない。例えば，太陽系天体の運動を扱うことを考えてみれば粒子数はせいぜいがO (10)個，惑星のみを扱うのならわずかに 9個である。筆者も各種の試行錯誤を繰り返したが，この程度の質点数ではベクトル化することによってむしろ計算速度が低下してしまう。また，質点数が少なすぎるため，計算の主要部分であり並列化が可能であると考えられる力関数行列計算の部分を頑張って並列化したつもりになっても，結局は前述の例のように台数効果がPE間通信に負けてしまい，非並列計算の方が速いということになってしまいそうである(図-10)。

しかしながら，視点を若干変えるだけでこうした常微分方程式の初期値問題を大変効率良く並列計算することができることがわかる。ここでのポイントは，並列化の作業を各粒子に関するものではなく，各刻み幅に関するものとして捉えることである¹⁸⁾。このアイディアを実現するのが補外法と呼ばれる計算手法である。

補外法の概念を述べてみよう。常微分方程式の初期値問題を数値的に解く場合，刻み幅,h を 0に近づけるに従って計算機上の仮想的な系が現実の物理系に近づいて行くと考えられる。このことを利用し，いくつかの有限のh を用いた数値積分によって得られた複数の解を多項式近似を用いて組み合わせ，h → 0の極限の値を外挿(補外)するのが補外法と呼ばれる数値解法である¹⁹⁾。Graggが考案したこの方法は従来の数値積分法に比べて極めて精度が良い²⁰⁾。更に，ある種の反復計算を行うことにより要求する範囲内で可能な限り精度の高い計算結果を得ることができるため，各種の天体暦のような精密計算に使用されて来た²¹⁾。

然るに補外法は計算量が大変に多く，惑星系の安定性を検証するといった長期の時間発展計算には向いていないと言われていた。だが良く考えてみると，補外法で使用される各h に対する計算はすべて独立であり，各々の間で干渉や通信を行うことなくまったく別個のPEで計算することができる。つまり，高い効率で並列化が有効なのである。

並列化補外法のアルゴリズム概略と計算結果の一例を示す(図-11，図-12)。補外の段数をn とした場合，数値積分の刻み幅は偶数系列(1/2n )でn 段取るのが普通である。今回はn = 8 の場合で実験したので，そもそも 8PE以上を使用してもそれ以上の高速化は望めない。また，各段の計算量は単純に 2n に比例するので，単純にn 段目をn 番目のPEに割り当てたのではPEごとの負荷が不均質になり，並列効果が薄くなる。

図-11

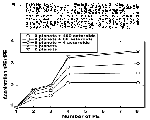図-12

そのため，我々は補外法並列化の部分について各段を折り返し(1と8，2と7などを組み合わせる)，各PEの負担を均一化する工夫をしている。これにより 4PE で 3.5倍近くの高速化が実現された。並列化とは殆ど縁がないと思われていた重力少体問題にとってこれは画期的なことである。

この補外法を用いて計算した外惑星軌道の約 1,000万年間の数値積分結果例を図-13に示した。冥王星の運動は海王星との間に奇妙な共鳴関係を保つことによって面妖な安定性を持続しており^{22), 23)},その運動を詳細に検証することによって惑星集積過程の謎を説き明かすことができるのではないかと期待されている。

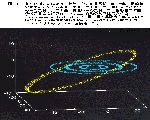図-13

従来，補外法の計算には非常に長い時間を要するため，重力少体問題の長期数値計算に於いては計算精度のチェックなどにのみ使用されて来た。けれども今後次第に並列計算機が普及するにつれ，並列化を行なった補外法が重力少体問題解法の主役に踊り出ることも十分に考えられる。なお，今回もデータ量が最大の場合(9惑星+400小惑星)が最高のPE台数効果を叩き出していることがわかる(図-12)。